Riproponiamo uno dei primissimi articoli apparsi sul nostro portale, nel lontano 2006. Dopo essere rimasto per troppo tempo nel nostro cassetto virtuale e dopo qualche aggiustamento, ecco a voi una bella panoramica sul concetto di overfishng, con qualche drammatico esempio ...Buona Lettura!

I pescatori non sono ricchi, nonostante le risorse biologiche del mar esiano fra le più indistruttibili e disponibili per l’uomo.

Qui giace la teoria del MSY, concesse di sfruttare una risorsa ma non spiegò come dividere la torta, la seppelliamo con i migliori auguri soprattutto a nome dei pesci futuri!
Peter Larkin, biologo marino.

L'OVERFISHING E I PROBLEMI DELLA SOVRAPESCA NEL MONDO - 1° parte

La maggior parte di noi è abituata a vedere il pesce solamente sui banconi del supermercato, l'ultima tappa di un breve viaggio che comincia nelle profondità del mare, luogo di nascita e morte per migliaia di pesci, ogni giorno.
Per avere un idea della problematica dell'overfishing, basti sapere che, se all’inizio del '900 il pescato mondiale ammontava a circa 5 milioni di tonnellate, nel 1990 ammontava a ben 86 milioni di tonnellate. Mentre la domanda è in continua crescita, soprattutto da parte dei paesi asiatici, commercialmente molto aggressivi, l'offerta dal 1990 è in calo in tutto il mondo. Il 1990 sembra essere stato l’anno della svolta, ma solo nel 1995, un articolo di C. Safina sul New Scientist, evidenziò nei dettagli la gravità del problema. Un articolo di D. Pauly e R. Watson, pubblicato sul numero 420 de Le Scienze dell'agosto 2003, porta un titolo esemplare "Fino all’ultimo pesce", così come appare esemplare il titolo dell’articolo pubblicato sul New Scientist del 12 gennaio 2002 "Thanks for all the fish".
Secondo la FAO, il 52% degli stock è sfruttato al limite, il 21% risulta moderatamente sfruttato, il 16% sovrasfruttato, il 7% esaurito, il 3% sottosfruttato e l’1% in recupero (Fonte: FAO 2003).
Ma procediamo per ordine. Innanzi il link in 'sitografia' rimanda a una pagina dove sono illustrati i modelli matematici utilizzati per lo studio della dinamica di popolazioni, sono spiegati i concetti di MSY, di overfishing, di sforzo di pesca e altro, per chi volesse approfondire. Qui tratteremo le stesse argomentazioni ma in modo più semplice e sintetico. Cominciamo illustrando il significato dell’acronimo MSY o Maximum Sustained Yield (Rendimento Massimo Sostenibile). Esso indica il massimo valore dello sforzo di pesca SY (Sustained Yield) che può essere mantenuto nel lungo periodo senza intaccare la consistenza e la capacità di rigenerazione delle popolazioni ittiche. In altri termini, indica il massimo numero di individui che possono essere prelevati ad intervalli regolari di tempo senza causare il declino della popolazione in questione. Se questo valore viene superato, si parla di overfishing o sovrasfruttamento nel caso dei pesci, oppure di overhunting nel caso di mammiferi marini come balene, delfini e foche.

ESEMPI DI OVERFISHING

L'esempio dell’eglefino e del merluzzo atlantico
Nel 1905 vennero attrezzati i primi pescherecci a vapore a tartana, con il compito di sfruttare le popolazioni di eglefino (Melanogrammus aeglefinus), un pesce demersale e oceanodromo, presso i grandi banchi denominati Georges Bank, colline sottomarine profondamente incise da antichi fiumi e dai ghiacci quando ancora erano emerse, durante l'ultima era glaciale, all’imboccatura del golfo del Maine, allora popolata da merluzzi ed eglefini in abbondanza.
La pesca non pianificata, proseguì anche durante la prima guerra mondiale e, nel 1929 furono pescate circa 120.000 tonnellate di eglefino. Ma gia nel 1934 il pescato si era ridotto del 77%, cioè a 28.000 tonnellate. Negli anni '60 gli eglefini furono spazzati letteralmente via dal golfo del Maine.
Nelle stesse zone di pesca, subì un calo considerevole anche la popolazione di merluzzi (Gados morhua), poiché le navi fattoria dislocate in quelle zone, verso la fine degli ann'70, prelevarono ben 810.000 tonnellate di merluzzi nel solo 1968, il triplo del pescato del miglior anno precedente.
Così, nel 1977 Canada e Stati Uniti estesero il limite delle acque territoriali a 200 miglia dalla costa, per allontanare dalle zone di pesca le enormi navi fattoria tedesche e sovietiche, nonché quelle di altri paesi come Germania e Spagna. Ebbero la possibilità di pianificare una corretta gestione delle risorse ittiche, ma non lo fecero. Il Canada, in particolare, si rivolse al DFO (Department of Fishieres and Oceans) che stimò, sulla base delle quote del 1978 (139.000 tonnellate), un pescato di 350.000 ton nel 1985, solo di fronte alle coste di Terranova. Di fronte ad una previsione del genere, furono molti a buttarsi nell'impresa, e le navi a tartana ripresero a solcare l’Atlantico. I primi anni '80 furono caratterizzati da un effettivo aumento del pescato e quest incoraggiò non poco i ricercatori del DFO, ma fu il primo errore. Il pescato infatti può essere in crescita anche di fronte ad un calo delle popolazioni ittiche. Il secondo errore, ammesso anni più tardi dal DFO, fu quello della sovrastima della popolazione in età riproduttiva (il merluzzo atlantico è maturo a 7 anni di età). Non permettendo ai pesci di raggiungere l’età della riproduzione, non è possibile incrementare gli stock ittici. Il terzo errore, il più grave, fu quello di non considerare l’effetto Allee (depensazione), secondo il quale la dinamica di una popolazione in calo demografico per effetto della sovrapesca o cause non naturali, non è paragonabile alla dinamica di una popolazione a bassa densità di individui, a cui corrisponde un maggior tasso di natalità. Per l'effetto Allee si ha esattamente l'opposto, se una popolazione è infatti in via di estinzione, il tasso di natalità tende a diminuire.
Nel 1991 l’epilogo e, nel 1992 molte zone di pesca furono chiuse e migliaia di persone persero il lavoro.
I ricercatori del DFO diedero la responsabilità della catastrofe a presunti eventi ambientali eccezionali (acque fredde, morie misteriose) e alcuni addirittura alle foche, così finanziarono l'uccisione di 250.000 individui per permettere alle popolazioni di merluzzi di riprendersi. Il New England, dopo il 1977, adottò la stessa politica del Canada, e il declino cominciò nel 1983, ma qui i ricercatori dell'NMFS (National Marine Fishery Service) sapevano che le popolazioni di merluzzi e eglefini erano in calo, ma il Consiglio del New England abolì addirittura le quote.
Solo nel 1991, con un azione legale da parte del CLF (Conservation Law Foundation) il Consiglio mutò atteggiamento con nuove regolamentazioni a partire dal 1994. Era gia troppo tardi e i danni della sovrapesca sono oggi alquanto evidenti. Come scrive Clover, il caso del merluzzo è un esempio da manuale di fallimento della scienza della pesca, nonostante una moltitudine di scienziati e di risorse economiche disponibili.
Come è andata a finire? In Canada il DFO continuò imperterrito con un errore dietro l’altro, stimando che entro il 1995 le riserve di merluzzi sarebbero state di nuovo abbondanti, cosa che non si è affatto verificata. Nel frattempo fu messa in pratica una pesca controllata (detta di "sentinella") fino al 2003, poi chiusa definitivamente per mancanza totale di merluzzi.

L'esempio delle sardine del Perù

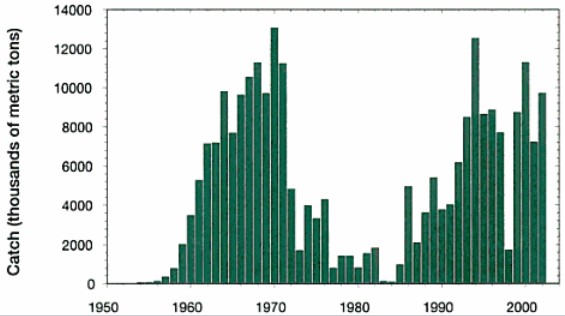
La costa occidentale del Sud America, è una delle poche zone di upwelling del mondo. In altri termini, acque fredde e profonde risalgono lungo la scarpata continentale, apportando in superficie quantità notevoli di nutrienti, tali da sostenere una produzione primaria elevatissima, il che significa moltissimo pesce.
Le zone di upwelling interessano solamente lo 0.5% degli oceani ma forniscono il 50% del pescato globale. In Perù, in particolare, la pesca del genere Sardina, Sardinops e Engraulis cominciò nei primi anni '50, con una stima del MSY di 10 milioni di tonnellate all'anno.
Nel 1967, il pescato dell'anchoveta Engraulis ringens, ammontava a 12.1 milioni di tonnellate. In effetti la crescita del pescato si mantenne elevata fino al 1971, poi nel 1972 ci fu il crollo dell'intera popolazione di sardine (grafico sopra).
La sardina peruviana o anchoveta, è un piccolo pesce che raggiunge la maturità sessuale entro il primo anno di vita e raramente supera i tre anni di età; dopo un anno, le sue dimensioni si aggirano attorno ai 12 cm. in lunghezza. Il reclutamento larvale coincide con la stagione primaverile australe; le larve si nutrono di plancton e tendono a concentrarsi nelle zone di mare relativamente fredde.
Il collasso della pesca dell'anchoveta, coincise con il famoso evento de El Niño che, come sappiamo, è spesso associato alle catastrofi ambientali peggiori e anche allora, come accade oggi, fu accusato del crollo della pescato. In realtà i peruviani si mostrarono ancor più fatalisti, il collasso della pesca infatti, coincise con l'assassinio di Brachero, un famoso imprenditore arricchitosi con le farine di pesce, per cui la sua morte venne associata a sventura e catastrifi. In effetti, il fallimento dell'azienda Brachero, venne seguito a ruota da tutte le altre aziende.
Anche la pesca dell'anchoveta è un classico esempio da manuale da non seguire. Il Perù e il Cile hanno gestito in modo sconsiderato e superficiale una preziosa risorsa del mare, peraltro per trasformare la quasi totalità del pescato in farine di pesce, fonte di preziosa valuta estera.
Sicuramente El Niño ha inciso sulla popolazione dell'anchoveta, almeno secondo l'Ipotesi del Match/Mismatch che illustro brevemente.
Come gia scritto sopra, le zone costiere del Cile e del Perù ricevono acque fredde e profonde, che risalgono la scarpata continentale, apportando una gran quantità di nutrienti. La ricchezza dei nutrienti, combinata con la giusta temperatura dell'acqua, determina massivi bloom fitoplanctonici che, successivamente, sono sfruttati dalle larve di una miriade di specie di pesci planctivori, tra cui l'anchoveta. El Niño, quando si "presenta", determina invece un anomalo riscaldamento superficiale delle acque costiere del sud america occidentale, per cui il picco (o bloom) fitoplanctonico, non coincide con il picco del massimo reclutamento larvale e, quindi, le larve non hanno sufficienti risorse trofiche e soccombono.

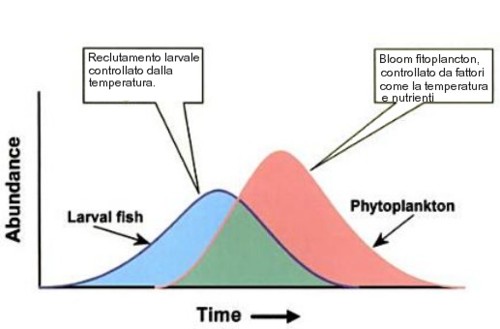
Esiste, o meglio, è stata ipotizzata, una reazione tra il tasso di reclutamento larvale e l'andamento del profilo della temperatura superficiale dell'acqua per molte specie ittiche.
Nel grafico sottostante è riportato il caso del salmone giapponese Oncorhynchus keta (Walbaum, 1792), meglio noto come Keta o salmone Keta (termine che deriva dalla lingua di alcune popolazioni Evenki, che vivono in Siberia e nel nord della Cina).

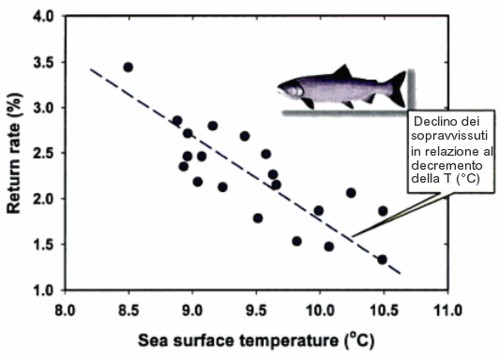
Se l'abbondanza di plancton è tale da consentire ai giovanili del salmone Keta di accrescersi e superare una taglia minima critica, entro il primo anno di vita, allora la popolazione sarà abbondante; al contrario, se a causa di variazioni importanti della temperatura superficiale del mare, il bloom fitoplanctonico è anticipato o ritardato, ecco allora che viene meno il reclutamento dei giovani salmoni.
Dunque El Niño ha sicuramente contribuito, ma di fatto le abbondanti catture dell'anchoveta non si sono ripetute, se non con qualche eccezione; di fatto la pesca di un tempo non è più neanche lontanamente immaginable ne sostenibile.

La sovrapesca in Italia
In Italia piani di intervento significativi non sono ancora stati intrapresi, anche se esistono delle proposte di intervento. Secondo alcuni è utile non tanto limitare le quote del pescato, per il fatto chè difficile controllare le catture e far rispettare le quote imposte. Meglio allora limitare i periodi di pesca durante l'anno e, al limite, diminuire il numero delle imbarcazioni e proibire completamente la pesca nelle aree costiere e di nursey, per salvaguardare gli esemplari giovanili e consentir loro di arrivare alla maturità.
La cattura eccessiva di esemplari giovanili è indicata come growth overfishing, che si contrappone al termine recruit overfishing, l'eccessiva cattura di esemplari adulti nel pieno delle loro capacità riproduttive.
Le specie in pericolo in Italia e nel Mediterraneo in generale, sono diverse. Una di queste è il tonno rosso (Thunnus thynnus, L.) che un tempo era numeroso in Adriatico durante le migrazioni stagionali, con al seguito squali bianchi e altri predatori pelagici.
La pesca non è più sostenibile e i dati a disposizione sono ambigui, spesso infatti viene catturato e posto in grandi gabbie offshore per l'allevamento. Da qui, dopo l’ingrasso, viene spedito direttamente a Tokio, al mercato ittico più grande del mondo.
Un'altra specie in declino è l’acciuga (Engraulis encrasicholus, L.) pesce che vive in grandi banchi e pescato in passato in grandi quantità in tutto il Mediterraneo con le lampare. Nel 1987 l’acciuga è collassata in Adriatico e ora in declino quasi ovunque. Altra specie è il pesce spada (Xiphias gladius, L.), che può raggiungere i 4 m. di lunghezza. Pur essendo proibita la pesca di esemplari sotto i 140 cm, esemplari sottomisura sono regolarmente commercializzati (basta tagliare la spada così da non poter risalire alle dimensioni reali), compresi gli esemplari giovani riconoscibili per aver pinne anali e dorsali uniche (sono duplici negli adulti).
In Adriatico è in diminuzione da oltre 10 anni anche la comune sardina (Sardina pilchardus, Walbaum), lo spinarolo (Squalus acanthias = Acanthias vulgaris, Risso) definito comune dal Soljan (Fishes of the Adriatic, 1963) ed ora sempre più raro, forse anche per cause diverse ma coeve all'overfishing; è in calo comunque in tutto il mondo. Altre specie in declino sono la triglia (Mullus surmuletus, L.) e il nasello (Merluccius merluccius, L. = Merluccius vulgaris, Fleming). Stanno scomparendo anche cernie, sgombri, spigole e cannochie. La spigola è diminuita quasi del 65 % in Adriatico. A rischio tutte le specie di squali e razze.

COME TI RASCHIO IL FONDO DEL BARILE

Un dato di fatto estremamente preoccupante, a cui si sta assistendo da qualche anno, è il prelievo di specie appartenenti a livelli trofici sempre più bassi, addirittura fino al krill, poiché, mancando le prede di maggiori dimensioni, che sono quelle a crescita lenta, per forza di cose si ricorre a individui più piccoli. A quest'ultima categoria di pesci appartengono sardine, aringhe e acciughe pescate in quantità enormi (corrispondenti a 49% del totale del pescato mondiale).
Pescare a livelli trofici così bassi significa togliere cibo ai pesci più grandi e quindi diminuire le loro chance di ripresa. Inoltre, solo metà dei piccoli pesci sono destinati al consumo umano, l'altra metà è trasformato in farine da utilizzare nell'acquacoltura e non solo, con enorme spreco di risorse. Basti pensare che per ottenere un chilo di salmone di allevamento, occorrono tre chili di farina di pesce [nel 2006, durante la stesura di questo articolo, non era ancora stato discusso ed approfondito il discorso sui rendimenti trofici, per approfondire, leggere qui]. È come l’allevamento dei bovini, per mantenerli all'ingrasso ed ottenere hamburger, occorre circa metà del raccolto di cereali degli Stati Uniti. Inoltre, pescare il krill, come sta facendo gia la Russia, significa intaccare la rete trofica direttamente alla base e alterare l’ecosistema in modo irreversibile.
Pianificare una politica di intervento per evitare il collasso dei territori di pesca, significa anche impegnarsi non solo nell'attuazione delle regolamentazioni, ma anche nella conoscenza della biologia delle singole specie. Conoscere significa appunto aver la possibilità di pianificare. Occorre sapere di ogni specie il ciclo vitale, quale posto occupa all’interno della rete trofica e di cosa si nutre in relazione all'età, occorre conoscere le zone che occupa, quali sono le aree di nursey; è importante anche conoscere le caratteristiche etologiche di ogni singola specie e il complesso delle relazione da essa instaurate con altre specie. Per esempio, non è ancora chiaro perchè merluzzi ed eglefini si raggruppano in banchi solamente quando le rispettive popolazioni sono in diminuzione.

PARTE SPECIALE -

IL MASSIMO RENDIMENTO SOSTENIBILE

Presentiamo ora un classico modello deterministico, noto come Modello di Produzione Equilibrata, o più semplicemente come Modello MSY. Si tratta di un modello semplice, il che ha decretato il suo successo in molte zone di pesca del mondo; in Mediterraneo non è stato molto applicato, con poche eccezioni, ad opera dei ricercatori dell'ISMAR.

Il rapporto ottimale tra stock ittico e sforzo di pesca è indicato con l'acronimo MSY (Maximum Sustained Yield), e indica il rendimento massimo sostenibile. Per capire bene di cosa si sta parlando, introduciamo alcuni semplici aspetti di dinamica delle popolazioni.
È noto che una popolazione ha, in natura, una capacità di crescita limitata (carrying capacity, capacità portante) oltre la quale il tasso di crescita tende a rimanere costante, a causa di fattori di varia natura che portano i tassi di natalità a eguagliare quelli di mortalità. Alcuni dei fattori che determinano questo stato di cose, sono detti fattori densità-dipendenti (density depended factors, ddf) e tra questi ricordiamo la predazione, le malattie, la diminuzione delle risorse, la competizione. Quindi inizialmente, quando la densità della popolazione è bassa, i suddetti fattori non incidono sulla crescita, cosa che invece diviene evidente oltre un certo valore soglia di densità (punto di flesso della figura sottostante):

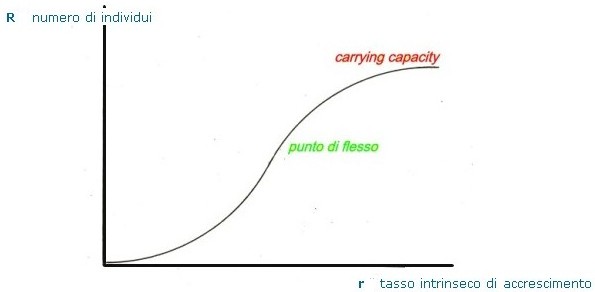
Abbiamo indicato con R il numero di individui di una popolazione, con r il tasso intrinseco di accrescimento, per cui la derivata di R rispetto al tempo vale:

dR / dt = rR (1 – R/K)

che non è atro che la curva sigmoide sopra riportata.
Nel caso in cui R = K la derivata è nulla, ossia la pendenza della curva vale zero, e siamo alla carrying capacity.
L'equazione sopra è detta equazione logistica. Il prelievo degli individui appartenenti ad una popolazione può essere fisso (sono prelevati un numero fisso di individui ad intervalli di tempo costanti), costante (una proporzione fissa di individui è prelevata ad intervalli di tempo costanti), oppure specifico (sono prelevate solo certe classi di età).
Il primo caso (prelievo fisso), riferendoci agli stock ittici, appartiene alla più semplice politica di prelievo adottata in passato e purtroppo anche oggi, da numerosi paesi. In tal caso, la sopravvivenza della popolazione dipende dal numero totale degli individui che la compongono inizialmente.
Esistono semplici modelli matematici elaborati allo scopo di determinare il massimo valore del prelievo fisso, in modo tale da non portare all’estinzione la popolazione. Occorre allora introdurre alcune semplici equazioni matematiche.
Indichiamo ancora con R il numero di individui di una popolazione (per esempio uno stock ittico di acciughe), con α la frazione dei nuovi nati e con β la frazione degli individui morti.
Il tutto sempre riferito all'unità di tempo (per esempio l’anno, indicato con t).
Allora determinare il numero di individui l'anno successivo (t+1) è semplice:

R(t+1) = R(t) + α R(t) – β R(t)

che si può scrivere come:

R(t+1) = (1 + α – β) R(t)

il termine (α – β) rappresenta il tasso di crescita specifica.
È facile notare che la popolazione sarà in crescita se α > β mentre sarà in diminuzione se α < β.
Se si interviene dall'esterno a disturbare l’andamento di questo trend, allora occorre introdurre un termine che indica la quantità di individui rimossi. Indicando con Y(t) tale quantità, si ha:

R(t+1) = (1 + α – β) R(t) – Y(t)

Se indichiamo con T il tasso di crescita (α – β) abbiamo:

R(t+1) = (1 + T ) R(t) – Y(t)

che possiamo riscrivere come:

R(t+1) = R(t) + T R(t) – Y(t)

Se quindi T R(t) > Y(t) la popolazione sarà in crescita e quindi R(t+1) > R(t),
oppure se T R(t) < Y(t) la popolazione sarà in diminuzione e quindi R(t+1) < R(t).
Affinché la popolazione sia in crescita, deve quindi verificarsi la condizione α >β.

Nel caso in cui una popolazione disponesse di quantità illimitate di risorse, e in assenza del prelievo Y(t), la sua crescita sarebbe esponenziale (tesi di Maltus 1798), cioè il suo tasso di crescita sarebbe proporzionale al numero di individui che la compongono.
È facile intuire che questa condizione non si verifica neanche in un ecosistema vasto e complesso come quello marino. Nella dinamica di crescita di una popolazione, il tasso di mortalità risulta dipendente dalla densità, per cui si suppone che β sia una frazione di R(t), per esempio NR(t).

R(t+1) = (1 + α – NR(t)) R(t)

Se in precedenza il tasso di crescita T era indicato come (α – β), ora diviene T1 = α –NR(t).
L'equazione generale di una retta è y = mx + q , ebbene il tasso di crescita densità-dipendente è una retta del tipo:

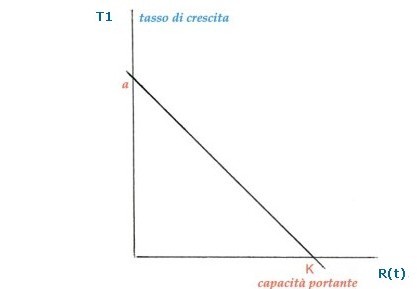
Il grafico riporta T1 in funzione di R(t) (tasso di crescita in funzione del numero di individui della popolazione). Notare che se R(t) = α/N, allora T1 è uguale a zero; tale particolare valore è indicato con K e indica ancora una volta la capacità portante o carrying capacity. Con l’introduzione del termine N cambia anche l’equazione R(t+1) = (1 + α – β) R(t) che diviene non lineare, e cioè:

R(t+1) = (1 + α –NR(t)) R(t)

R(t+1) = R(t) + αR(t) –NR(t²)

R(t+1) = (1 + α) R(t) – NR (t²)

Quest'ultima è un'equazione non lineare rappresentata da una parabola ed è detta curva di crescita non logistica F:

F = (1 + α) R(t) – NR (t²)

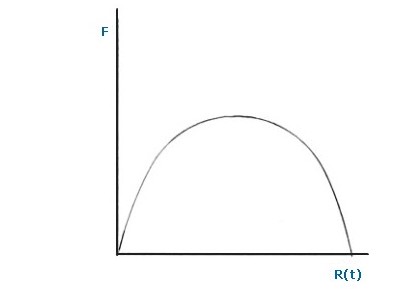
Notare che all’istante t = 0, F interseca l’origine degli assi, mentre interseca di nuovo l'asse delle x quando R(t) = (1 + α) / N.
In conclusione, il modello ci informa che anche riducendo una popolazione a pochi individui, la sua capacità riproduttiva la porterebbe di nuovo a livelli di equilibrio, fino al raggiungimento della capacità portante. Tale tesi è stata a lungo sostenuta da vari scienziati, ed è tuttora ostinatamente proposta in ambienti "poco" scientifici. Nel caso di un prelievo fisso, occorre aggiungere all’equazione R(t+1) = (1 + α –NR(t)) R(t) il numero di individui prelevati annualmente, indicati in precedenza con Y(t). Abbiamo:

R(t+1) = (1 + α –NR(t)) R(t) – Y(t)

Il grafico è ancora una parabola, ma traslata verso il basso di una quantità Y. Questo, ovviamente, indica che maggiore è il prelievo, e maggiore sarà lo spostamento verso il basso della curva. L’equazione qui sopra ha due soluzioni, ma ci addentreremo in passaggi matematici abbastanza noiosi. Quello che è importante evidenziare, è che con il metodo del "prelievo fisso" la popolazione all’equilibrio assume valori di densità inferiori (è ovvio) a quelli che assumerebbe se non sfruttata, a patto che la biomassa (il numero di individui della popolazione indicato con R) non scenda sotto un valore soglia Rs, determinabile attraverso la soluzione dell’equazione di secondo grado qui sopra.
Nel caso di un prelievo costante o a sforzo costante (fishinf effort), il modello si complica ulteriormente. Occorre introdurre un termine e che indica lo sforzo di pesca e un valore, detto coefficiente tecnologico TC, che tiene conto delle migliorie tecnologiche introdotte nell’unità di tempo. L’equazione diviene allora:

R(t+1) = (1 + α – e TC - NR(t)) R(t)

L'equazione è ancora una parabola passante per l’origine degli assi. L’equilibrio R(t+1) = R(t), si ottiene se R(t) = 0 o se R(t) = (α – e TC) / N. Sostituendo infatti quest'ultimo valore all'equazione R(t+1) = (1 + α – e TC - NR(t)) R(t), si vedrà che R(t+1) = R(t) = (α – e TC) / N. Questo particolare valore all'equilibrio della popolazione sottoposta ad uno sforzo costante, è indicato con Ke e può essere confrontato con la capacità portante di una popolazione non sfruttata. Ricordiamo che K = α/N, mentre Ke = (α – e TC) / N.

Quindi, se α > e TC, l’equilibrio Ke rimane positivo e stabile, mentre se α < e TC, l’equilibrio diviene instabile e si ha estinzione della popolazione nel lungo periodo. Il prodotto SY = e TC Ke è detto produzione sostenibile (suistainable yield).
Vediamo di studiare questa equazione. Se poniamo SY = 0 si ottiene che e = α / TC oppure e = 0. La stessa equazione è positiva per valori di 0 < e < α / TC, mentre è nulla per valori di e > α / TC. Infine se e = α / 2TC, si ottiene un valore di SY che è il nostro MSY o MAXIMUM SUSTAINED YIELD, che corrisponde alla massima produzione che può essere mantenuta nel lungo periodo, e che coincide con lo sforzo di pesca e_MSY.

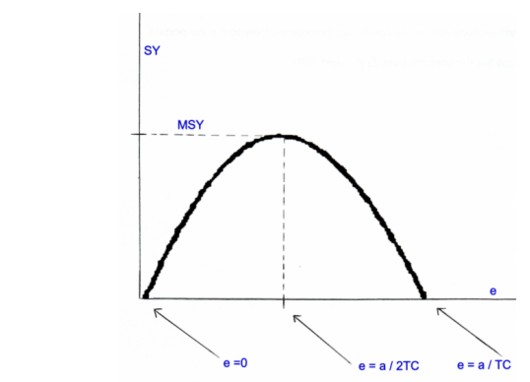
In tutti quei casi dove lo sforzo di pesca, nel lungo periodo, supera il valore di MSY, si parla di overfishing o sovrasfruttamento.

Siamo giunti alla capacità portante K per definire finalmente il massimo prelievo sostenibile MSY, inteso come il massimo numero di individui che può essere prelevato a intervalli regolari senza causare il declino della popolazione in questione.
Si ha:

MSY = ( K/2) T - K/2

Il primo termine ( K/2) T indica la popolazione R al tempo (t + 1), mentre il secondo termine indica la popolazione R al tempo (t). Come si arriva a questo risultato?
Il limite del modello non è "matematico" ma sta nel fatto che non è possibile:

• (i) avere valori attendibili del numero iniziale di individui di una popolazione;
• (ii) stimare le catture non autorizzate;
• (iii) prevedere eventi accidentali che incideranno sullo stock della popolazione.

Il primo punto può essere messo in discussione da chiunque, nel senso che le stime sulla struttura di una popolazione sono diverse a seconda della fonte, l'esperienza a proposito insegna moltissimo, in ogni caso saranno e sono state gonfiate da chi ha interesse ad aumentare lo sforzo di pesca, con le conseguenze che tutti possiamo immaginare.
_____________________

La parte speciale e le formule utilizzate sono state tratte da un lavoro che risultava disponibile online nel 2006. In data odierna non siamo purtroppo riusciti a rintracciare la stessa fonte. Scusandoci per l'inconveniente, rimaniamo a disposizione con gli aventi diritto e i titolari dell'eventuale licenza.

AGGIUNGI UN COMMENTO [Se non desideri visualizzare il tuo commento sul tuo profilo Facebook, ricordati di togliere la spunta della ceckbox]

BIBLIOGRAFIA

• Gian Italo Bischi - Modelli matematici e risorse rinnovabili: il dilemma del pescatore e altri apparenti paradossi.
• Maurizio Melis - Inchiesta sul mondo della pesca. Speciali di Aqva.
• Barkai A., Bergh M. - Modelli di popolazione più complessi per la valutazione degli stock, strutturati per età e taglia.
• C. Clover - Allarme Pesce. Ponte alle Grazie, 2005.

ARTICOLI CORRELATI

• LE SPECIE PIÙ PREZIOSE DEL PIANETA
• PESCA ILLEGALE DEL MERLUZZO ANTARTICO, SILENZIO DALLA CITES
• CECKLIST DELLE SPECIE ITTICHE DA EVITARE
• IL MARE DEL MADAGASCAR SACCHEGGIATO DAI BRACCONIERI STRANIERI
• AQUACALYPSE NOW, intervista a D. Pauly parte I
• AQUACALYPSE NOW, intervista a D. Pauly parte II
• Il saccheggio delle risorse ittiche in Africa parte I & parte II
• Il saccheggio delle risorse ittiche in Africa parte III
• La mafia della pesca
• I DATI SULLA PESCA ILLEGALE DELLA COMMISSIONE EUROPEA